[백준 Python] - 6588 골드바흐의 추측
- Data Science/PS (Python)
- 2024. 4. 14.
250x250
728x90
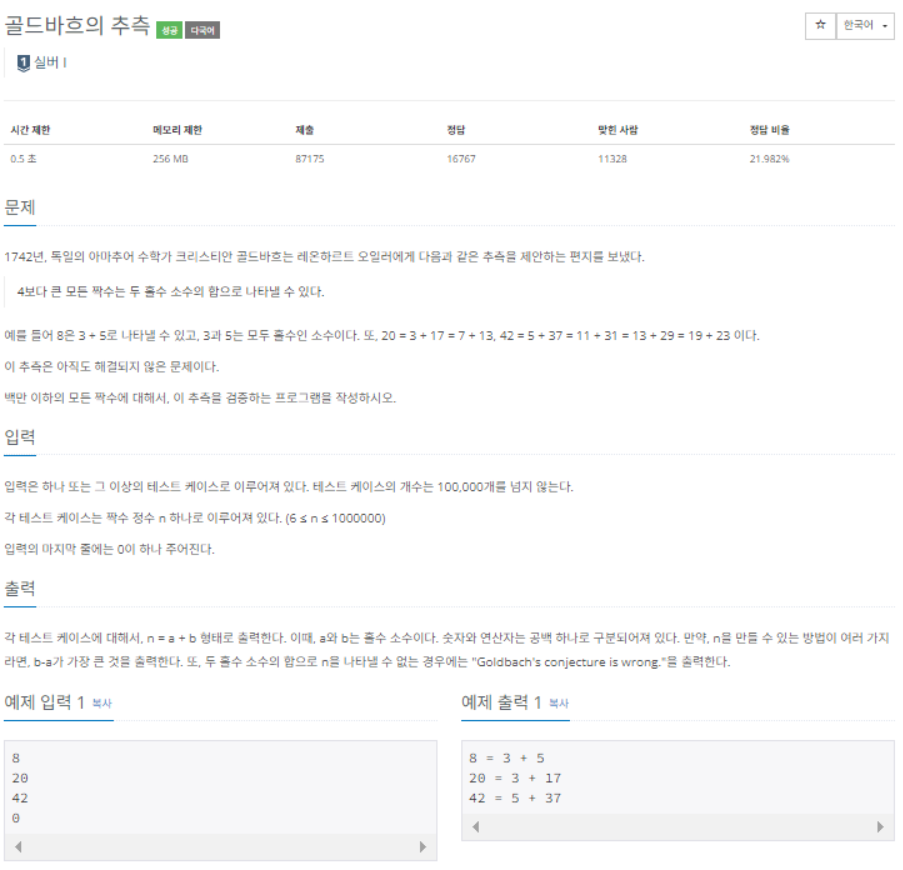
1. 문제 - 6588번
2. 접근법
기존에 풀었던 에라토스테네스의 체를 활용해 풀 수 있었다. (참고 : 백준 문제 11653)
풀이 과정은 다음과 같다.
- 우선 에라토스테네스의 체를 이용해 문제에서 주어진 범위(6 <= n <= 1000000)를 포괄하는 소수 집합을 구한다
-> 이렇게 하지 않고 각 케이스마다 소수 집합을 새로 만들 경우, 코드 실행에 엄청난 초과 시간이 소요된다.
- 구한 소수 집합을 바탕으로, 작은 값부터 시작해, 특정 소수 및 n - 특정소수 가 모두 존재하는지 확인한다.
<정답 코드>
import sys
input = sys.stdin.readline
def prime_num(n): # 에라토스테네스의 체 -> 소수 집합 구하기
primes = [True]*n
primes[0] = False
primes[1] = False
for i in range(2, int(n*0.5)+1):
if primes[i]:
for j in range(2*i, n, i):
primes[j] = False
return primes
def test_goldbach(n, prime_list):
for index, prime in enumerate(prime_list): # 짝수 n = 소수 a + 소수 b 일때, a와 b의 차가 최대가 되는 소수 집합은 a의 값이 최소일 때
prime_sync = n - index
if prime and prime_list[prime_sync]:
return f"{n} = {index} + {prime_sync}"
else:
return "Goldbach's conjecture is wrong."
primes = prime_num(1000000) # 이렇게 미리 최대 범위의 소수 집합을 구해놓는 것이 오히려 코드 실행을 빠르게 한다
while True:
n = int(input())
if n == 0:
break
print(test_goldbach(n, primes))728x90
'Data Science > PS (Python)' 카테고리의 다른 글
| [Python 자료구조] 간단한 이진 탐색 트리(BST, Binary Search Tree) 구현하기 (0) | 2024.05.07 |
|---|---|
| [백준 Python] - 2004 조합 0의 개수 (0) | 2024.04.11 |
| [백준 Python] - 1676 팩토리얼 0의 개수 (0) | 2024.04.10 |
| [백준 Python] - 10872 팩토리얼 (0) | 2024.04.10 |
| [백준 Python] - 11653 소인수분해 (0) | 2024.04.10 |